In questa lezione vedremo la codifica e le conversione binarie. Analizzeremo i cambi di base e capiremo come si comporta il nostro calcolatore nei suoi calcoli.

L’informazione

ℹ️ Informazione → E’ un messaggio che trasporta conoscenza. Rappresenta un dato + significato. Può essere un’immagine, un suono (notizia, ambiente circostante).

Un’informazione può essere elaborata: modificata, misurata, registrata, controllata…

Il calcolatore riesce ad elaborare un’informazione solo se:

• L’informazione sia codificata opportunamente (numericamente);
• Le elaborazioni da compiere sono descritte in modo algoritmico (sequenze finite di passi elementari).

Codificare un’immagine 🖼

• Ad ogni punto facciamo corrispondere un numero che ne codifica il livello di grigio;
• Mettendo di seguito tutte le cifre di tali numeri in un ordine prestabilito, l’immagine è codificata.

Il bianco è rappresentato dal 255, il nero dallo 0, i grigi sono i valori di mezzo.

Codificare il suono 🔊

• La percezione del suono è causata dalla variazione nel tempo, della pressione dell’aria in prossimità del timpano.
• La pressione si può misurare (convertire in numero) a intervalli di tempo piccoli (campionamento), i valori sono numeri…

Per rappresentare un’informazione, associamo al significato un simbolo (Codifica). L’operazione inversa è chiamata interpretazione.

Le codifiche possono essere diverse:

• Codifica ridondante: “La penna può essere chiamata penna o biro.” L’interpretazione è univoca;
• Codifica ambigua: l’interpretazione NON è univoca. Si fa riferimento al contesto. “Per penna possiamo riferirci al tipo di pasta, alle penne dell’uccello…”

Codifica numeri interi

Codifica decimale (dec, in base dieci);

A = { 0,1,2,3,4,5,6,7,8,9}

|A| = dieci

138 = 1 * 10^2 + 3 * 10^1 + 8*10^0 oppure centotrentotto

La notazione decimale è di tipo posizionale NON ambigua e NON ridondante.

Notazioni non posizionali: numeri romani → II, III, IV, V, XX, (NON ambigua, ridondante).

Base = otto → A = { 0,1,2,3,4,5,6,7} → 29 dec = 35 baseotto = 38^1 + 58^0

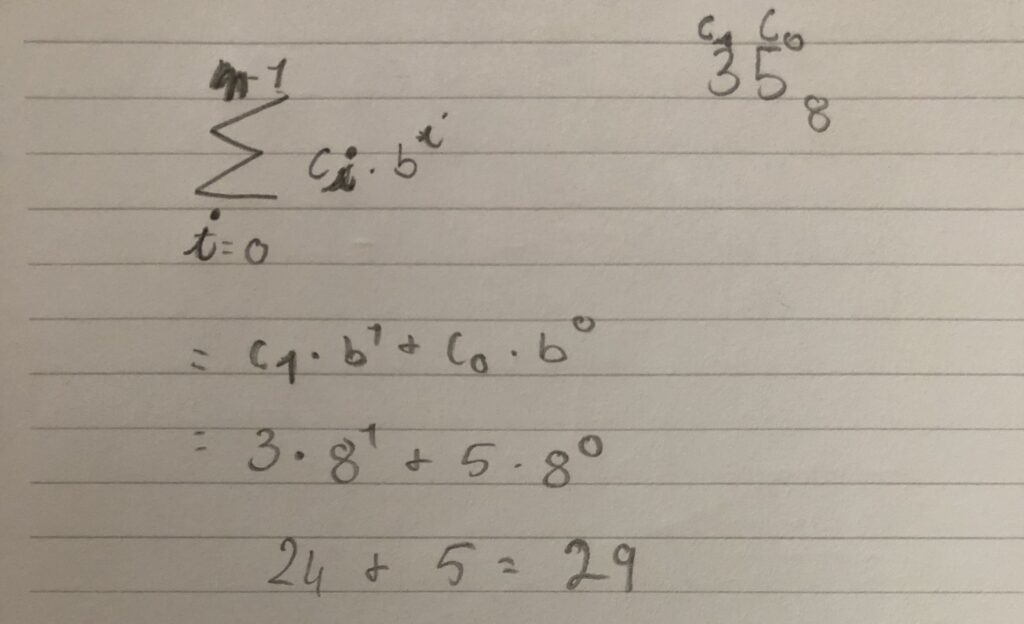
Base = cinque → A = { 0,1,2,3,4} → 29 dec = 104 basecinque = 45^0 + 05^1 + 1*5^2;

Base = tre → A = { 0,1,2,} → 29 dec = 1002 basetre;

Base = sedici → A = { 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F} → 29 dec = 1D base16 = 1**16^1 + D16^0 = 16 + 13 (D occupa la posizione 13).

Codifica Binaria

B = due, A = {0, 1}

Dispositivi che assumono due stati (Alto e Basso).

2️⃣ BIT → Binary digit. 8 bit formano un byte

Con n bit codifichiamo 2^n numeri interi positivi: da 0 a 2^n – 1.

Da Binario a Decimale

00000000 bin = 0 dec

00001000 bin = 1 * 2^3 = 8 dec

00101011 bin = 02^7 +02^6 +1 * 2^5 + 02^4 + 1 * 2^3 + 02^2 + 12^1 + 1 2^0 = 43 dec

11111111 bin = 255 dec

Da Decimale a Binario – Metodo dei resti (algoritmo)

19 : 2 = 9 resto 1

9 : 2 = 4 resto 1

4 : 2 = 2 resto 0

2 : 2 = 1 resto 0

1 : 2 = 0 resto 1

19 dec = 10011 bin

Dividiamo il numero per la base (in questo caso è 2) e si tiene il resto. Il quoziente si divide per la base e si tiene il resto, finché il quoziente non diventa 0. Si leggono i resti dal basso verso l’alto componendo così il numero binario (in questo caso).

Esempio da Decimale a base Sei

29 : 6 = 4 resto 5

4 : 6 = 0 resto 4

29 dec = 45 sei

Conversioni rapide bin → dec

K = 2^10 = 1024 → 10^3 (Kilo)

Mi = 2^20 = 1048576 → 10^6 (Mega)

Gi = 2^30 = 1.073.741.824 → 10^9 (Giga)

T = 2^40 = 1.099.511.627.776 → 10^12 (Tera)

Quanto vale 2^17? → 2^7 + 2^10 = 128 + 1024 = 128K = 128 * 10^3  Quanto vale 2^24 ? → 2^20 + 2^4 = 16M

Operazioni sui numeri binari

Non possono esserci bit vuoti, essi sono o VA o VB (valore alto o basso).

Se aggiungiamo gli 0 davanti al numero binario, il numero non cambia 100bin = 00000100 bin. Possiamo ridurre un numero binario rimuovendo gli 0 davanti ad esso.

Somma tra numeri binari

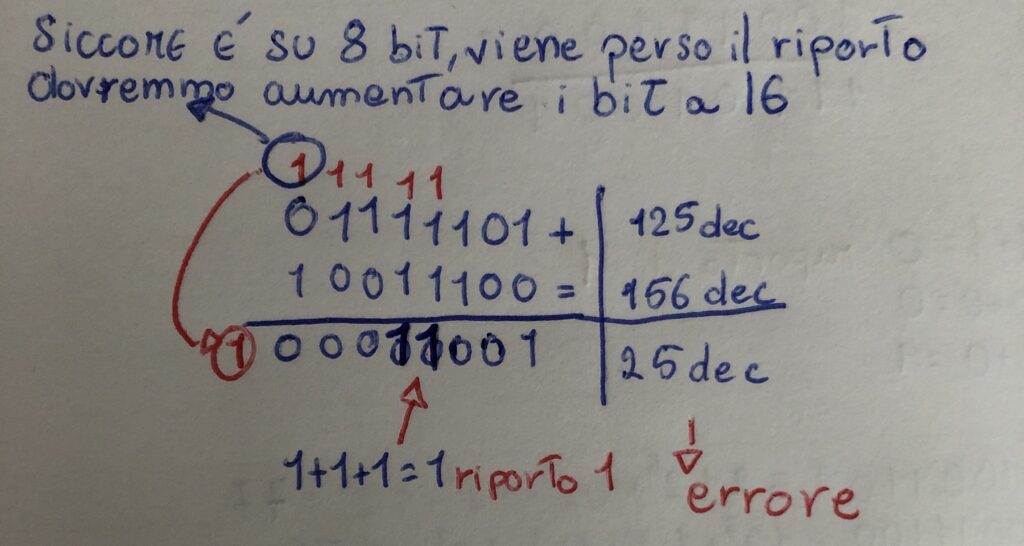
⁉️ overflow → Quando il risultato corretto eccede il potere di rappresentazione dei bit a disposizione. Significa che il valore del risultato non può essere rappresentato con il numero di cifre a disposizione. Tipicamente si aumenta il numero di bit da 8 a 16. Il risultato è quindi un’operazione errata.

Binario → Ottale

binario → ottale 000 bin → 0 oct, 001 → 1, 010 → 2, 011 → 3, 100 → 4, 101 → 5, 110 → 6, 111 → 7.

La conversione da binario a ottale si ottiene raggruppando il numero binario in gruppi di tre da destra verso sinistra:

1011110 bin = (1)(011)(110) = 136 oct

Da ottale a decimale:

35 oct = 38^1 + 58^0 = 29 dec

Binario → Esadecimale

binario → HEX 0000 bin → 0 hex, 0001 → 1, 0010 → 2, 0011 → 3, 0100 → 4, 0101 → 5, 0110 → 6, 0111 → 7, 1000 → 8, 1001 → 9, 1010 → A, 1011 → B, 1100 → C, 1101 → D, 1110 → E, 1111 → F.

La conversione da binario a esadecimale si ottiene raggruppando il numero binario in gruppi di 4 da destra verso sinistra:

1011010101 bin = (10) (1101) (0101) = 2D5 HEX

Da HEX a decimale

1A2 HEX = 116^2 + 1016^1 + 216^0 =* 418 dec

Numeri frazionari in virgola fissa (fixed point)

0,1011 bin → 02^0 + 1 * 2^-1 + 02^-2 + 12^-3 + 02^-4 = 1/2 +1/8 + 1/16 = 0,6875 dec.

Si hanno 5 bit per la parte intera e 4 bit per la parte dopo la virgola.

Dec frazionario in binario

Per passare da 0,6875 dec in 0,1011 bin:

• Moltiplico per 2 la parte frazionaria.
• tengo il resto e moltiplico la parte frazionaria;
• Mi fermo se ottengo 1 come risultato della moltiplicazione (senza resto da poter moltiplicare);
• Leggo le parti intere nell’ordine in cui le ho ottenute.

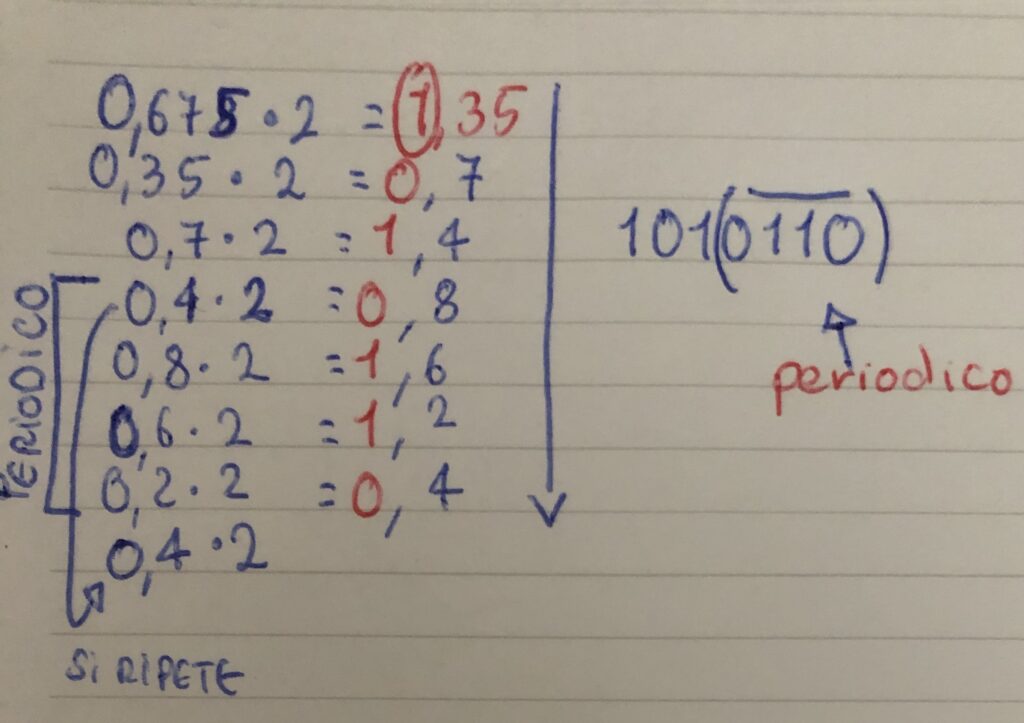
Se ho 6,2 dec, per passare in bin si converte prima il 6 da dec a bin normalmente e poi si converte la parte decimale con il metodo sopra illustrato.

Numeri frazionari in virgola mobile (floating point)

si utilizza la notazione scientifica. 0,137 * 10^8 = 13.700.000

Ci consente di rappresentare, come la notazione scientifica, sia numeri molto grandi che numeri molto piccoli.

• Bisogna stare attenti alla precisione nelle rappresentazioni. (Facile fare errori).

R(virgola mobile) = M * B^e

• M = mantissa, numero frazionario compreso tra (-1 e 1) → m > 1 bit → numero di bit che possiamo usare per rappresentare il numero (ci deve venir dato).
• B = Base non rappresentata (implicita)
• N bit > 1 per l’esponente e → numero di bit che possiamo usare per rappresentare l’esponente (ci deve venir dato).
• Si usano M + N bit

🚧 Il segno è rappresentato in modulo e segno → è un bit esterno che si aggiunge dopo. 0 positivo, 1 negativo. E’ indicato con s

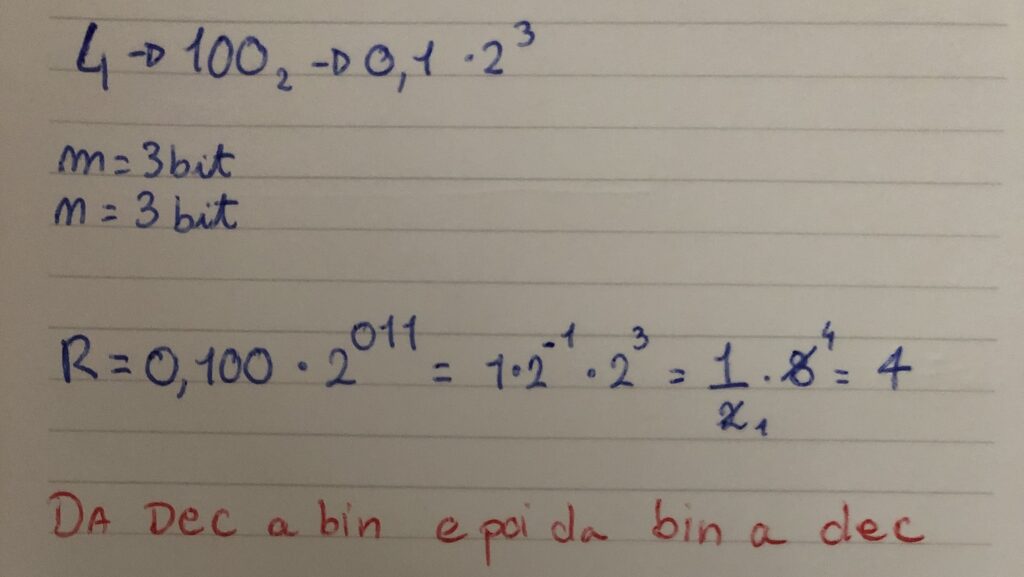
Standard per i numeri

IEEE 754 è uno standard che definisce:

• i formati di rappresentazione binario naturale, C2 e virgola mobile (le m e le n);
• Gli algoritmi di somma, sottrazione e prodotto;
• I metodi di arrotondamento;
• Come trattare gli errori (overflow, divisione per 0, radice quadrata di numeri negativi);

Standard per i caratteri

ASCII (american standard computer interchange interface) è uno standard per i caratteri a 7 bit per la lingua inglese (non più utilizzato) o a 8 bit per il resto delle lettere accentate;

ISO -X rappresenta i sistemi di scrittura internazionali;

Codifica UNICODE → codice universale a 16 bit che contiene tutti i caratteri (ideogrammi…)

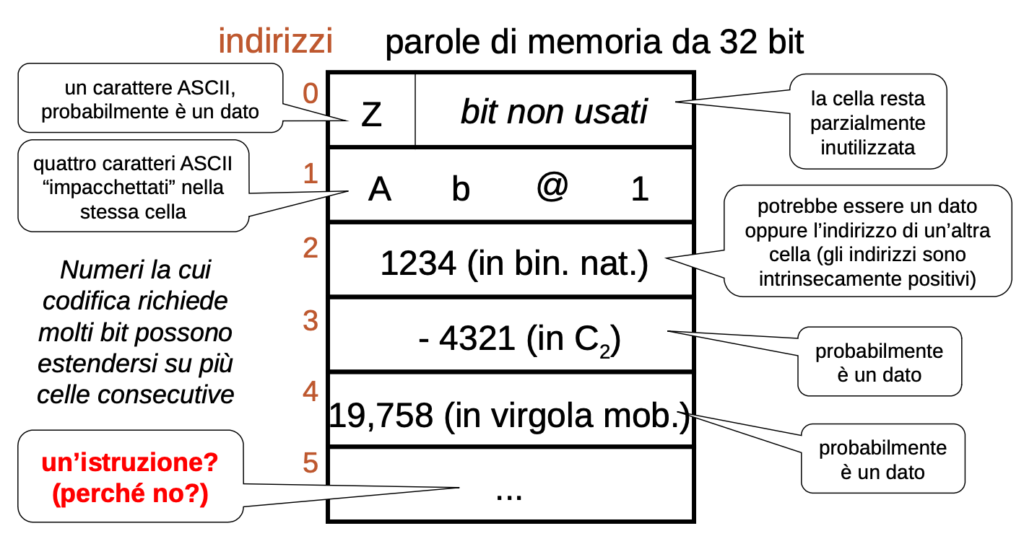
Rappresentazione di una parola

Una parola di memoria è in grado di contenere una sequenza di n bit. Di solito n = 8, 16, 32 o 64 bit.

Essa indica come vengono trasportati i dati tra memoria e calcolatore; può contenere:

• Un carattere (o più di uno);
• Un numero intero in binario naturale o in C2;
• Un numero frazionario in virgola mobile;
• Alcuni bit possono essere non usati.